Uber H3 Index

23 May 2020 - 4 minute read

Abstract

• given a latitude/longitude point, find the index of the containing H3 cell at a particular resolution
• given an H3 index, find the latitude/longitude cell center
• given an H3 index, determine the cell boundary in latitude/longitude coordinates

Overview

The H3 grid is constructed on the icosahedron by recursively creating increasingly higher precision hexagon grids until the desired resolution is achieved. Note that it is impossible to tile the sphere/icosahedron completely with hexagons; each resolution of an icosahedral hexagon grid must contain exactly 12 pentagons at every resolution, with one pentagon centered on each of the icosahedron vertices.

Base Cells

The first H3 resolution (resolution 0) consists of 122 cells (110 hexagons and 12 icosahedron vertex-centered pentagons), referred to as the base cells.

Resolution

Each subsequent resolution beyond resolution 0 is created using an aperture 7 resolution spacing (aperture refers to the number of cells in the next finer resolution grid for each cell); as resolution increases the unit length is scaled by \sqrt{7}7 and each hexagon has 1/7th the area of a hexagon at the next coarser resolution (as measured on the icosahedron).

H3 provides 15 finer grid resolutions in addition to the resolution 0 base cells. The finest resolution, resolution 15, has cells with an area of less than 1 m^2.

H3 Index

IJK Coordinate

Discrete hexagon planar grid systems naturally have 3 coordinate axes spaced 120° apart. We refer to such a system as an ijk coordinate system, for the three coordinate axes i, j, and k. A single ijk coordinate triplet is represented in the H3 Core Library using the structure type CoordIJK

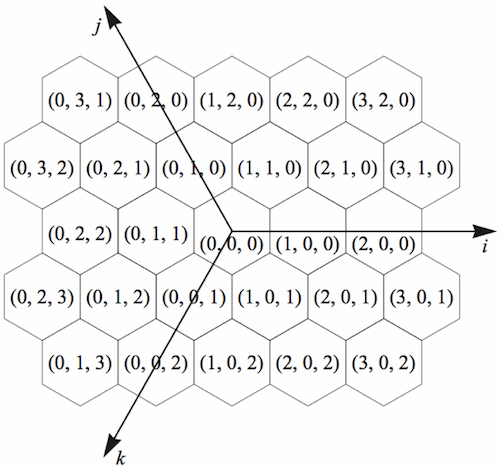
1.0 unit distance in the Hex2d system is the distance between adjacent cell centers in the ijk coordinate system.

Index Representation

The H3Index is the integer representation of an H3 index, which can be placed into multiple modes to indicate the kind of concept being indexed. Mode 1 is an H3 Cell (Hexagon) Index, mode 2 is an H3 Unidirectional Edge (Hexagon A -> Hexagon B) Index, mode 3 is planned to be a bidirectional edge (Hexagon A <-> Hexagon B). Mode 0 is reserved and indicates an invalid H3 index.

However, only mode 1 will be used in RCS Demo.

The components of the H3 cell index (mode 1) are packed into a 64-bit integer in order, highest bit first, as follows:

• 1 bit reserved and set to 0,
• 4 bits to indicate the index mode,
• 3 bits reserved and set to 0,
• 4 bits to indicate the cell resolution 0-15,
• 7 bits to indicate the base cell 0-121, and
• 3 bits to indicate each subsequent digit 0-6 from resolution 1 up to the resolution of the cell (45 bits total are reserved for resolutions 1-15)

Bit layout of H3Index

The layout of an H3Index is shown below in table form. The interpretation of the “Reserved/edge” field differs depending on the mode of the index.

	0x0F	0x0E	0x0D	0x0C	0x0B	0x0A	0x09	0x08	0x07	0x06	0x05	0x04	0x03	0x02	0x01	0x00
0x30	Reserved	Mode	Reserved/edge	Resolution	Base cell
0x20	Base cell			Digit 1			Digit 2			Digit 3			Digit 4			Digit 5
0x10			Digit 6			Digit 7			Digit 8			Digit 9			Digit 10
0x00		Digit 11			Digit 12			Digit 13			Digit 14			Digit 15

Experiment

I have picked 2 points in Nanjing City: [37.7076131999975672,-122.5123436999983966] and [37.813318999983238,-122.4089866999972145] and then checked the index of them form resolution 0 to resolution 15.

it is easy to see the bit layout in H3 Index.

no. bit	meaning
0	reserved bit and default to 0
1-4	mode 1
5-7	since we only use mode 1, it was reserved and set to 0
8-11	resolution level
12-18	the base cell
19-63	ijk coordinator from resolution 1 - 15, thus the total is 3*15

Redis Key Design

According to the H3 concept and the experiment that we have, we can find once we get 15th resolution we can get all parents’ ijk coordinate information. Thus, we can keep the 15th resolution index to construct the Redis key which is in binary format.

[7 bits base cell info(resolution 0)] + [15 ijk coordinate info(resolution 1 - 15)]

For the points in the experiments, once we call h3 api geoToH3() we can get the index as follow:

point 1: 0 0001 000 1111 0010100 000110000100000001101110010110000000110011010

point 2: 0 0001 000 1111 0010100 000110000100101000000011001110101001101000000

==> find the keys:

key 1: 0010100000110000100000001101110010110000000110011010

key 2: 0010100000110000100101000000011001110101001101000000

Conclusion:

• key length is 52 bits,
• unique key for each point,
• compact the original index,
• easy to query aggregation and union

Method Design

In RCS Backend Cloud project, the Hexagon.class provides a method to generate compact index.

    public static String getCompactHexagonKey(double lat, double lng) {
        
        String binaryIndex = String.format("%64s", new BigInteger(getMaxHexagonKey(lat, lng), 16).toString(2))
                .replace(" ", "0").substring(12);
        int face = Integer.parseInt(binaryIndex.substring(0, 7), 2);
        StringBuilder sb = new StringBuilder(String.valueOf(face));

        for(int i = 7; i < binaryIndex.length(); i+=3) {
            sb.append(String.valueOf(Integer.parseInt(binaryIndex.substring(i, i+3),2)));
        }
        return sb.toString();
    }