线性结构索引——从数组和链表的原理初窥检索本质
数组结构需要连续空间来存储,而链表不需要。
数组和链表分别代表了连续空间和不连续空间的最基础的存储方式,它们是线性表(Linear List)的典型代表。其他所有的数据结构,比如栈、队列、二叉树、B+ 树等,都不外乎是这两者的结合和变化。

使用二分法提升数组的检索效率:通过排序转为有序的数据集。
合理地组织数据的存储可以提高检索效率。检索的核心思路,其实就是通过合理组织数据,尽可能地快速减少查询范围。
链表在检索和动态调整上的优缺点
但是使用链表,似乎也无法通过排序来提高检索的效率,因为链表是非连续的地址空间。链表检索能力偏弱,作为弥补,它在动态调整上会更容易。
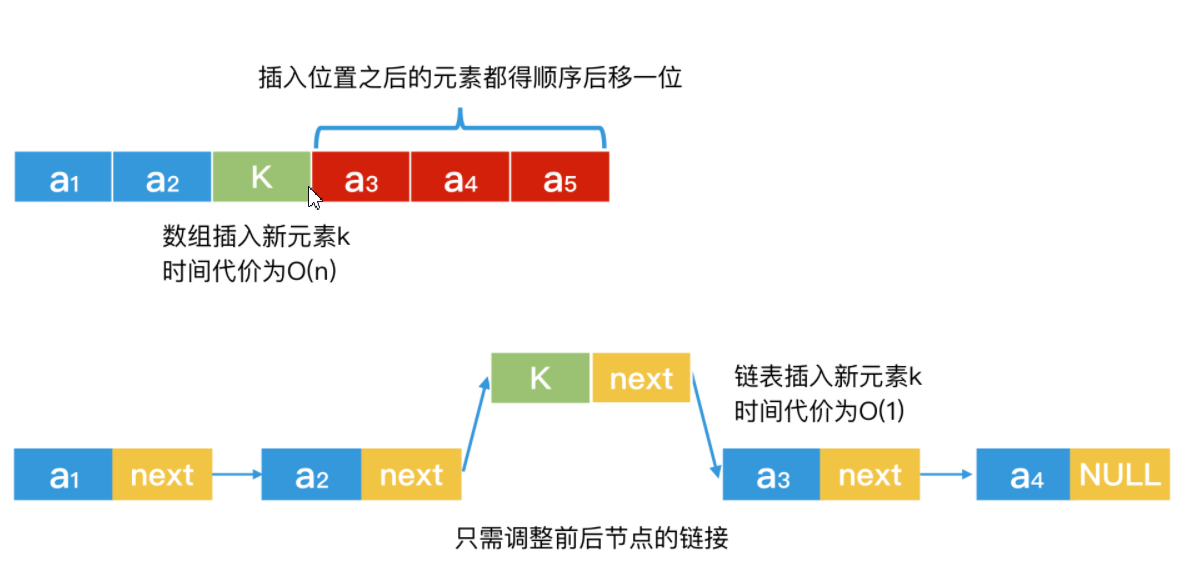
如何灵活改造链表提升检索效率——“非连续存储空间“的组织方案
对于“非连续空间”,可以用指针将它串联成一个整体。我们应该在不同的应用场景中,设计出适用的数据结构,而不是拘泥于链表自身的结构限制。
一个简单的改造例子
比如说,如果我们觉得链表一个节点一个节点遍历太慢,或许我们可以想到一个解决方案就是让链表每个节点不再只是存储一个元素,而是存储一个小的数组。

假设只有两个节点,每个节点都存储了一个小的有序数组,在检索时就通过二分查找的思想,先查询第一个节点存储的小数组的末尾元素,然后决定是去到下一个节点,还是我们查询的元素就在此节点上。OlogN
Q&A
为什么使用二分查找算法,而不是 3-7 分查找算法,或 4-6 分查找算法?
对于单个查询值 k,我们已经熟悉了如何使用二分查找。那给出两个查询值 x 和 y 作为查询范围,如果要在有序数组中查找出大于 x 和小于 y 之间的所有元素,我们应该怎么做呢?
二分查找是你在不了解数据分布时的最佳策略,37和46都有靠运气假设的成分。
第一种方法是先二分查找x,然后二分查找y,x和y之间的元素就是答案了。第二种方法就是只二分查找x或者y,然后去顺序遍历,和另一个去比较。
对x和y分别做两次二分查找,时间代价为log(n)+log(n)。 而对x做二分查找,再遍历到y,时间代价为log(n)+(y-x)。 发现没有,我们完全可以根据log(n)和(y-x)的大小进行预判,哪个更快就选哪个! 当然,除非y-x非常小,否则一般情况下log(n)会更小。