倒排索引加速2:对联合查询进行加速
方法1:调整次序法
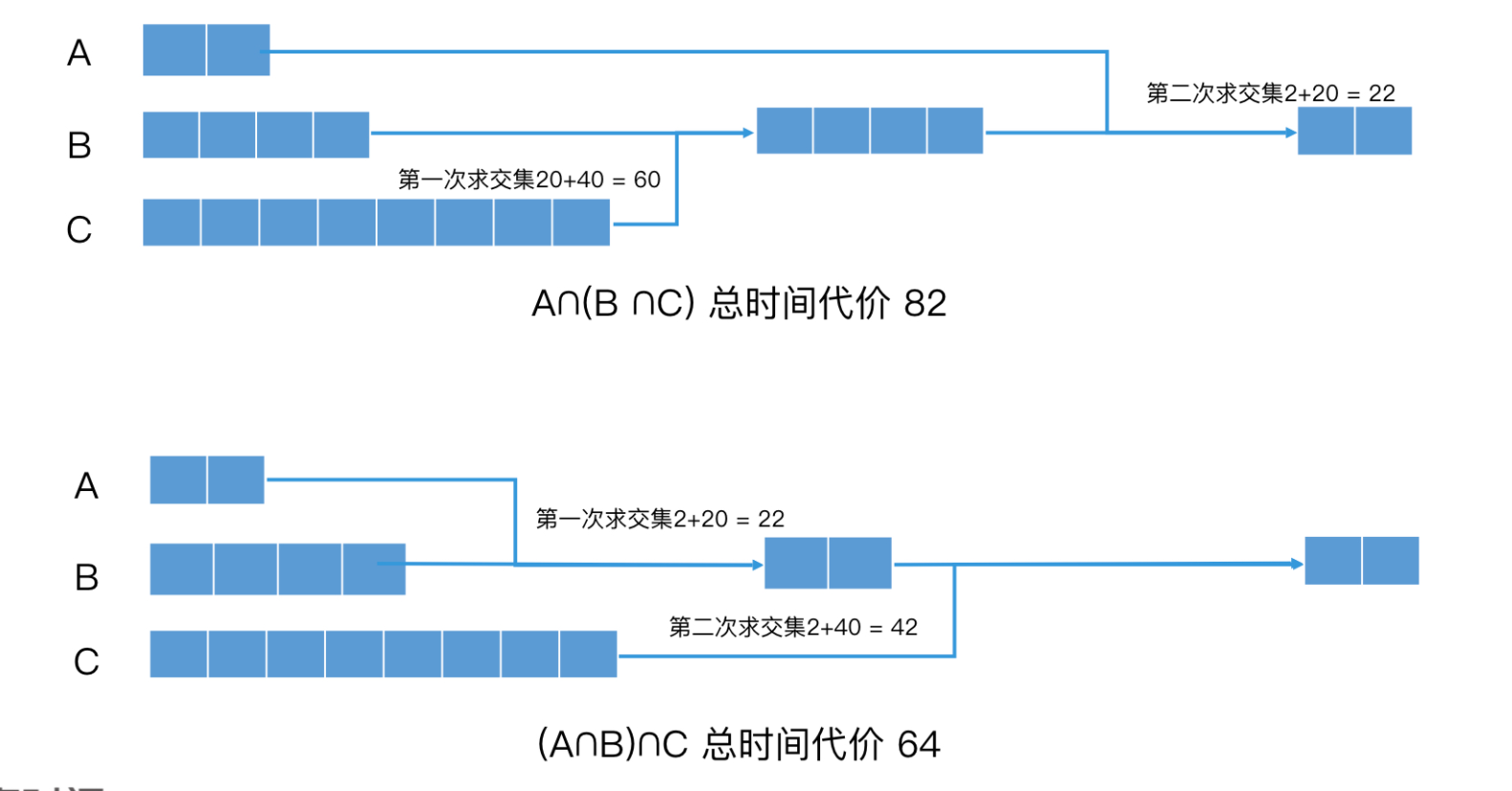
A∩(B∩C)、(A∩B)∩C要如何调整次序。假设A、B、C的元素个数分别是2、20、40,且A包含咋洗B内,B包含在C内。
- A∩(B∩C)B和C求交集时间代价就是 20+40 = 60,得到的结果集是 B,然后 B 再和 A 求交集,时间代价是 2 + 20 = 22。因此,最终一共的时间代价就是 60 + 22 = 82。
- (A∩B)∩C 时,我们要先对 A 和 B 求交集,时间代价是 2 + 20 = 22,得到的结果集是 A,然后 A 再和 C 求交集,时间代价是 2 + 40 = 42。因此,最终的时间代价就是 22 + 42 = 64。这比之前的代价要小得多。
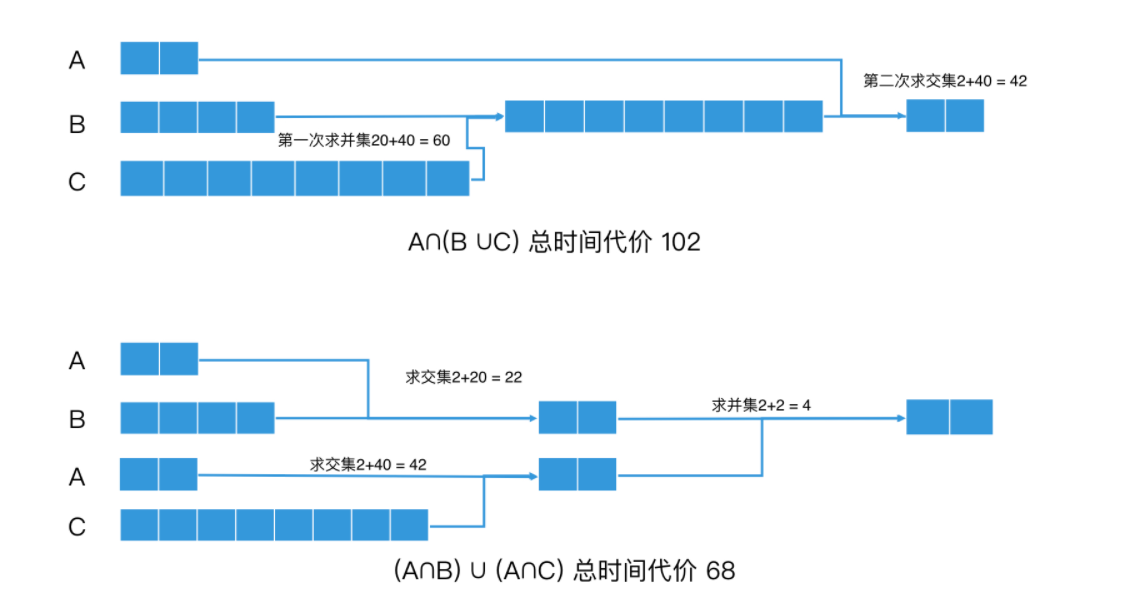
计算A ∩(B∪C),如果不做任何优化,∪C 的操作,时间代价是 20 + 40 = 60,结果是 C。然后再和 A 求交集,时间代价是 2+40 = 42。一共是 102。
分配率公式:A∩(B∪C)=(A∩B)∪(A∩C)
我们要执行 A∩B 操作,时间代价是 2+20 = 22,结果是 A。然后,我们执行 A∩C 操作,时间代价是 2+40=42,结果也是 A。最后,我们对两个 A 求并集,时间代价是 2+2=4。因此,最终总的时间代价是 22 + 42 + 4 = 68。这比没有优化前的 102 要低得多。
如果有一个例子(B∪C∪D∪E∪F),那我们用分配律改写的时候,A 就需要分别和 B 到 F 求 5 次交集,再将 5 个结果求并集。这样一来,操作的次数会多很多,性能就有可能下降。因此,我们需要先检查 B 到 F 每个集合的大小,比如说,如果集合中元素个数都明显大于 A,我们预测它们分别和 A 求交集能有提速的效果,那我们就可以使用集合分配律公式来加速检索。
方法2:快速多路归并法
在对多个 posting list 求交集的过程中,我们可以利用跳表的性质,快速跳过多个元素,加快多路归并的效率。这种方法,我叫它“快速多路归并法”。它的实现方式就是将 n 个链表的当前元素看作一个有序循环数组list[n]。并且,对有序循环数组从小到大依次处理,当有序循环数组中的最小值等于最大值,也就是所有元素都相等时,就说明我们找到了公共元素。
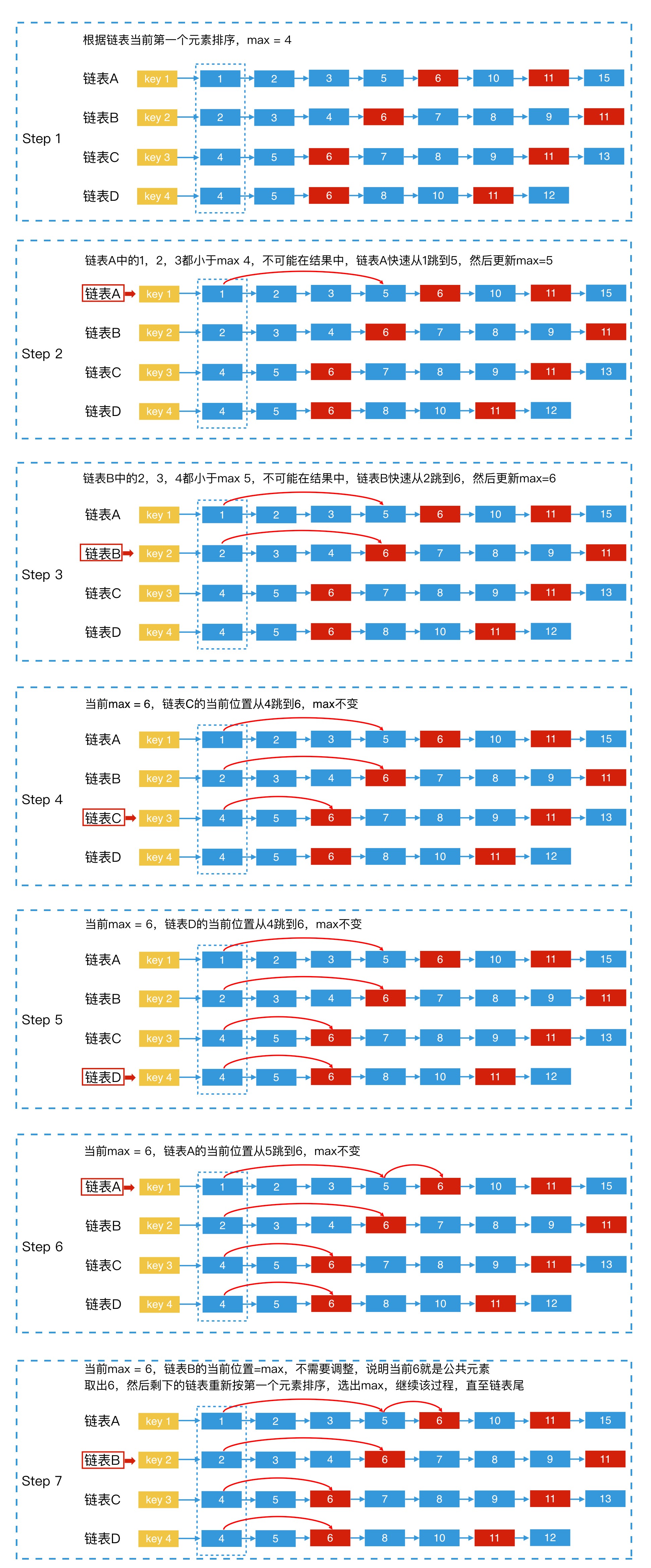
For example, 我们要对4个链表A、B、C、D求交集,具体的实现步骤为:
- 将 4 个链表的当前第一个元素取出,让它们按照由小到大的顺序进行排序。然后,将链表也按照由小到大有序排列
- 用一个变量 max 记录当前 4 个链表头中最大的一个元素的值
- 从第一个链表开始,判断当前位置的值是否和 max 相等:
- 如果等于max,说明此时所有链表的当前元素都相等,该元素为公共元素,那我们就将该元素去除,然后回到第一步。
- 如果当前位置的值小于 max,则用跳表法快速调整到该链表中第一个大于等于 max 的元素位置
- 如果新位置元素的值大于max,更新max的值
- 对下一个链表重复第 3 步,就这样依次处理每个链表(处理完第四个链表后循环回到第一个链表,用循环数组实现),直到链表全部遍历完。
方法3:预先组合法
其实预先组合法的核心原理,和我们熟悉的一个系统实现理念一样,就是能提前计算好的,就不要临时计算。
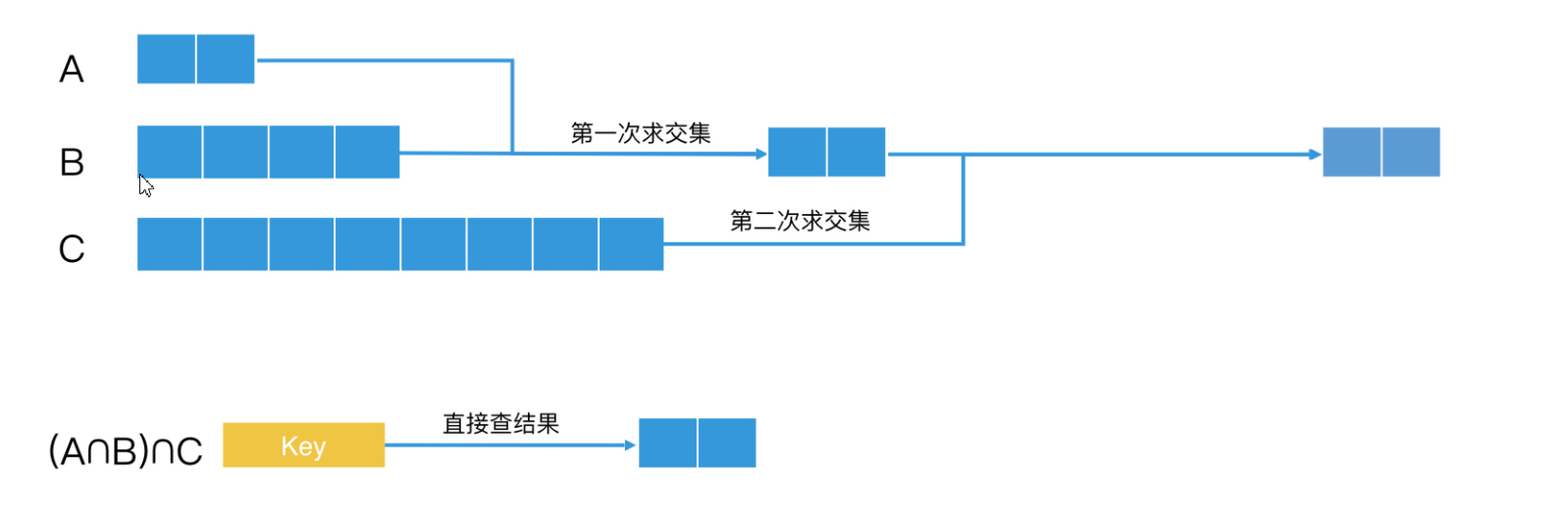
假设,key1、key2 和 key3 分别的查询结果是 A、B、C 三个集合。如果我们经常会计算 A∩B∩C,那我们就可以将 key1+key2+key3 这个查询定义为一个新的组合 key,然后对应的 posting list 就是提前计算好的结果。之后,当我们要计算 A∩B∩C 时,直接去查询这个组合 key,取出对应的 posting list 就可以了。
方法4:缓存法加速联合查询
方法3的前提是需要预先知道提前要查询的内容,但是很多时候回出现一些最新的查询组合,我们可以使用缓存技术来优化。
- 缓存技术就是指将之前的联合查询结果保存下来。这样再出现同样的查询时,我们就不需要重复计算了,而是直接取出之前缓存的结果即可。这里,我们可以借助预先组合法的优化思路,为每一个联合查询定义一个新的 key,将结果作为这个 key 的 posting list 保存下来。
- 我们还要考虑一个问题:内存空间是有限的,不可能无限缓存所有出现过的查询组合。因此,对于缓存,我们需要进行内容替换管理。一种常用的缓存管理技术是LRU(Least Recently Used),也叫作最近最少使用替换机制。所谓最近最少使用替换机制,就是如果一个对象长期未被访问,那当缓存满时,它将会被替换。
对于最近最少使用替换机制=,方案可以是:
- 使用双向链表:当一个元素被访问时,将它提到链表头。这个简单的机制能起到的效果是:如果一个元素经常被访问,它就会经常被往前提;如果一个元素长时间未被访问,它渐渐就会被排到链表尾。这样一来,当缓存满时,我们直接删除链表尾的元素即可。
- 如果想要快速查询缓存,我们可以使用 O(1) 查询代价的哈希表来优化。我们向链表中插入元素时,同时向哈希表中插入该元素的 key,然后这个 key 对应的 value 则是链表中这个节点的地址。这样,我们在查询这个 key 的时候,就可以通过查询哈希表,快速找到链表中的对应节点了。因此,使用“双向链表 + 哈希表”是一种常见的实现 LRU 机制的方案。
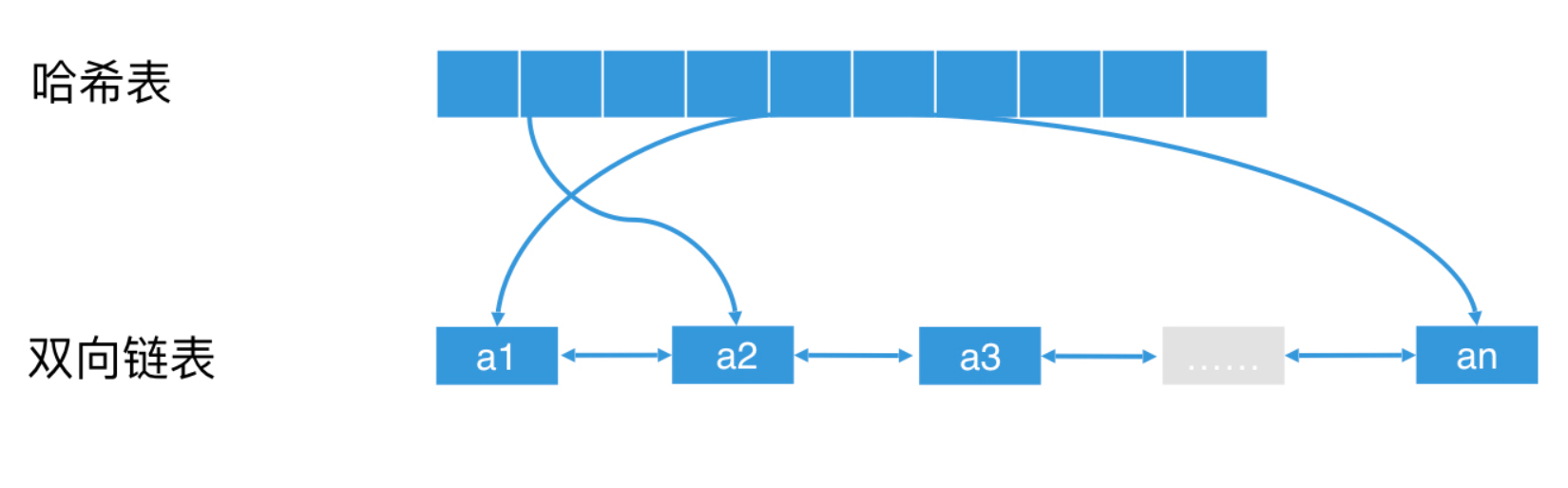
通过使用 LRU 缓存机制,我们就可以将临时的查询组合缓存起来,快速查询出结果,而不需要重复计算了。一旦这个查询组合不是热点了,那它就会被 LRU 机制替换出缓存区,让位给新的热点查询组合。缓存法在许多高并发的查询场景中,会起到相当大的作用。比如说在搜索引擎中,对于一些特定时段的热门查询,缓存命中率能达到 60% 以上甚至更高,会大大加速系统的检索效率。