哈希检索——根据ID快速查询用户信息
使用hash函数将key转换为数组下表
如果系统中的用户ID是从1开始到10000的整数,可以通过数组来实现O(1)级别的查询能力。

那如果内存空间有限,我们只能开辟一个存储 10000 个元素的数组该怎么办呢?这个时候,我们可以使用“tom”对应的数值 149123 除以数组长度 10000,得到余数 9123,用这个余数作为数组下标。这就是hash。
但是数组空间是有限的,值要被Hash的元素个数大于数组上限,就一定会产生冲突。解决方案:
- 构造尽可能理想的 Hash 函数,使得 Hash 以后得到的数值尽可能平均分布,从而减少冲突发生的概率
- 在冲突发生以后,通过“提供冲突解决方案”来完成存储和查找。
开放寻址法(Open Addressing)
“线性探查”(Linear Probing)的插入逻辑很简单:在当前位置发现有冲突以后,就顺序去查看数组的下一个位置,看看是否空闲。如果有空闲,就插入;如果不是空闲,再顺序去看下一个位置,直到找到空闲位置插入为止。
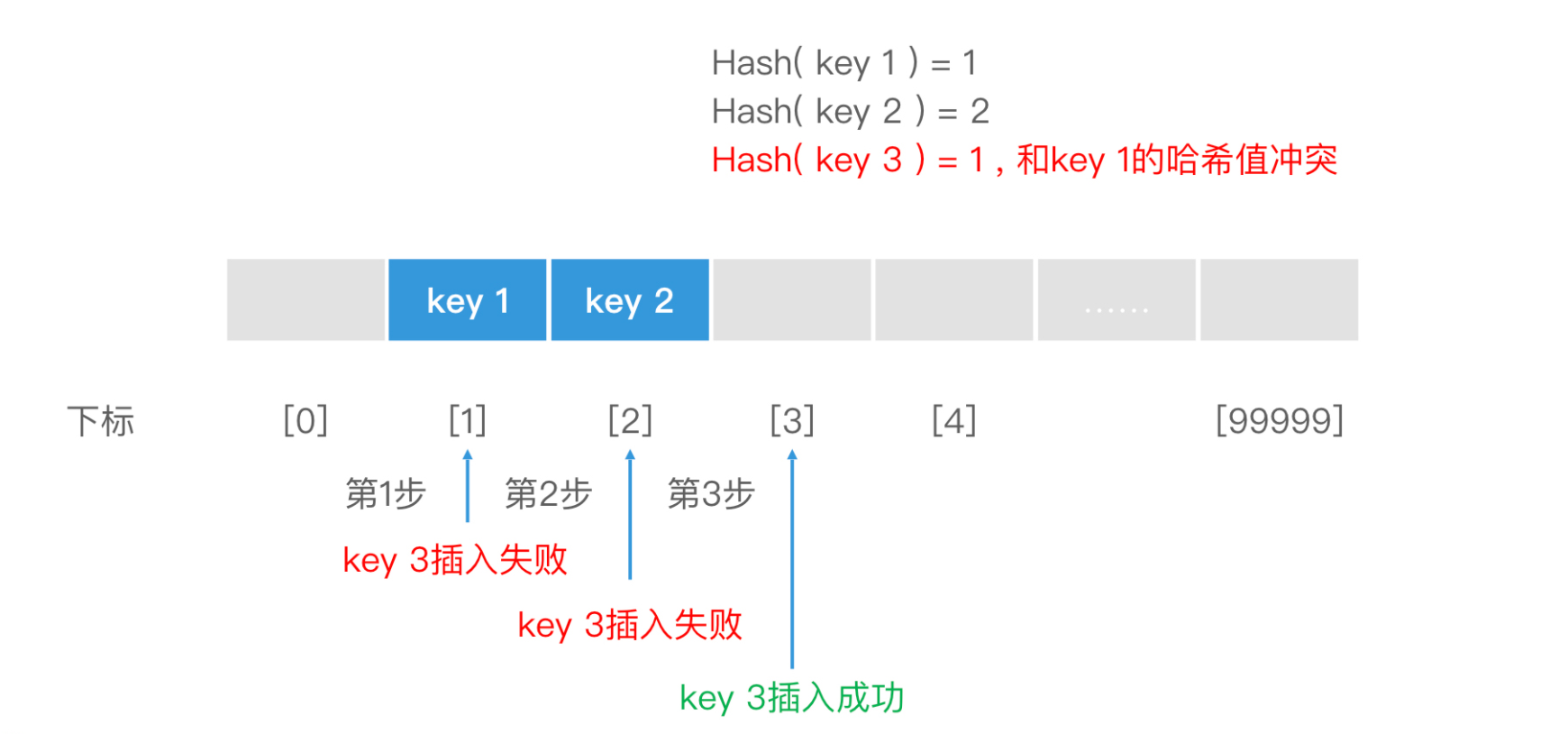
当我们插入一个 Key 时,如果哈希表已经比较满了,这个 Key 就会沿着数组一直顺序遍历,直到遇到空位置才会成功插入。查询的时候也一样。但是,顺序遍历的代价是 O(n),这样的检索性能很差。
更糟糕的是,如果我们在插入 key1 后,先插入 key3 再插入 key2,那 key3 就会抢占 key2 的位置,影响 key2 的插入和查询效率。因此,“线性探查”会影响哈希表的整体性能,而不只是 Hash 值冲突的 Key。
为了解决这个问题,我们可以使用“二次探查”(Quadratic Probing)和“双散列”(Double Hash)这两个方法进行优化:
- 二次探查就是将线性探查的步长从 i 改为 i^2:第一次探查,位置为 Hash(key) + 1^2;第二次探查,位置为 Hash(key) +2^2;第三次探查,位置为 Hash(key) + 3^2,依此类推。双散列就是使用多个 Hash 函数来求下标位置,当第一个 Hash 函数求出来的位置冲突时,启用第二个 Hash 函数,算出第二次探查的位置;如果还冲突,则启用第三个 Hash 函数,算出第三次探查的位置,依此类推。
- 双散列就是使用多个 Hash 函数来求下标位置,当第一个 Hash 函数求出来的位置冲突时,启用第二个 Hash 函数,算出第二次探查的位置;如果还冲突,则启用第三个 Hash 函数,算出第三次探查的位置,依此类推。
无论是二次探查还是双散列,核心思路其实都是在发生冲突的情况下,将下个位置尽可能地岔开,让数据尽可能地随机分散存储,来降低对不相干 Key 的干扰,从而提高整体的检索效率。RE-HASH
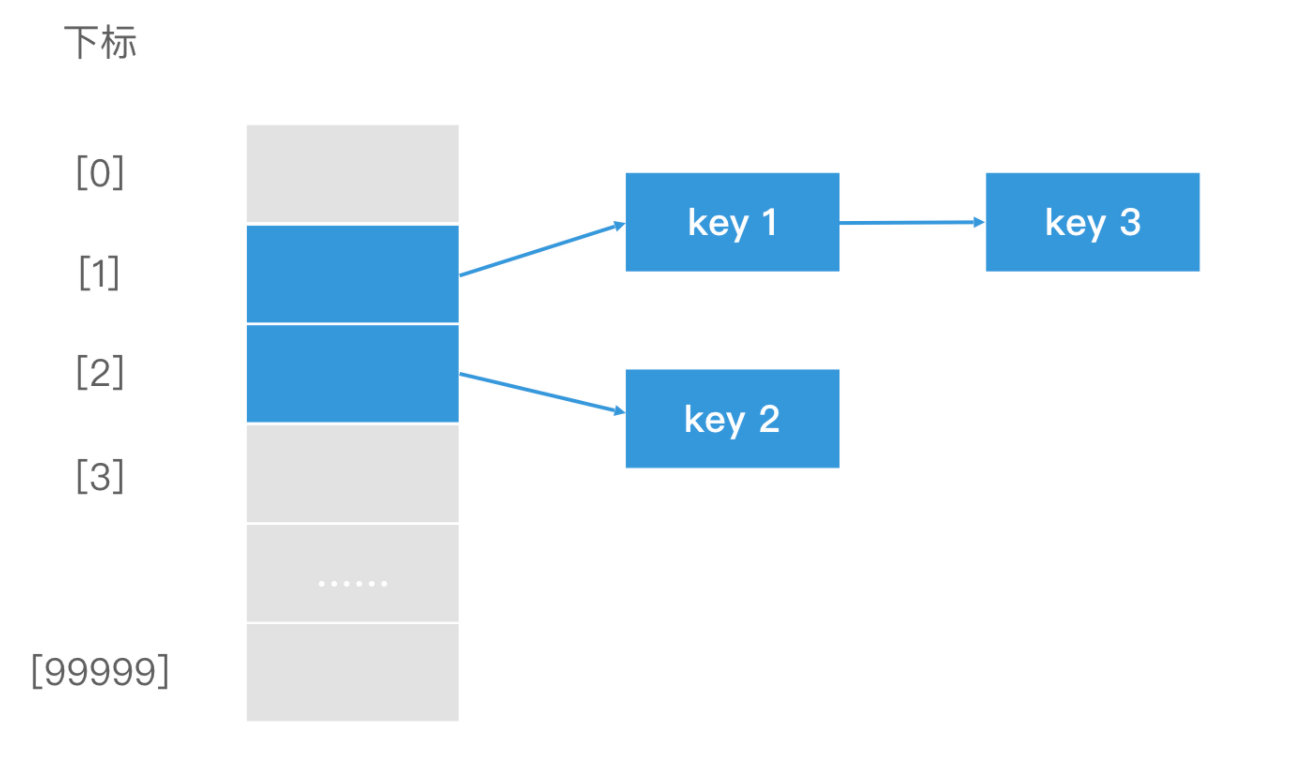
链表法解决Hash冲突
如果 key3 和 key1 发生了冲突,那么 key3 会通过链表的方式链接在 key1 的后面,而不是去占据 key2 的位置。这样当 key2 插入时,就不会有冲突了。最终效果如下图。
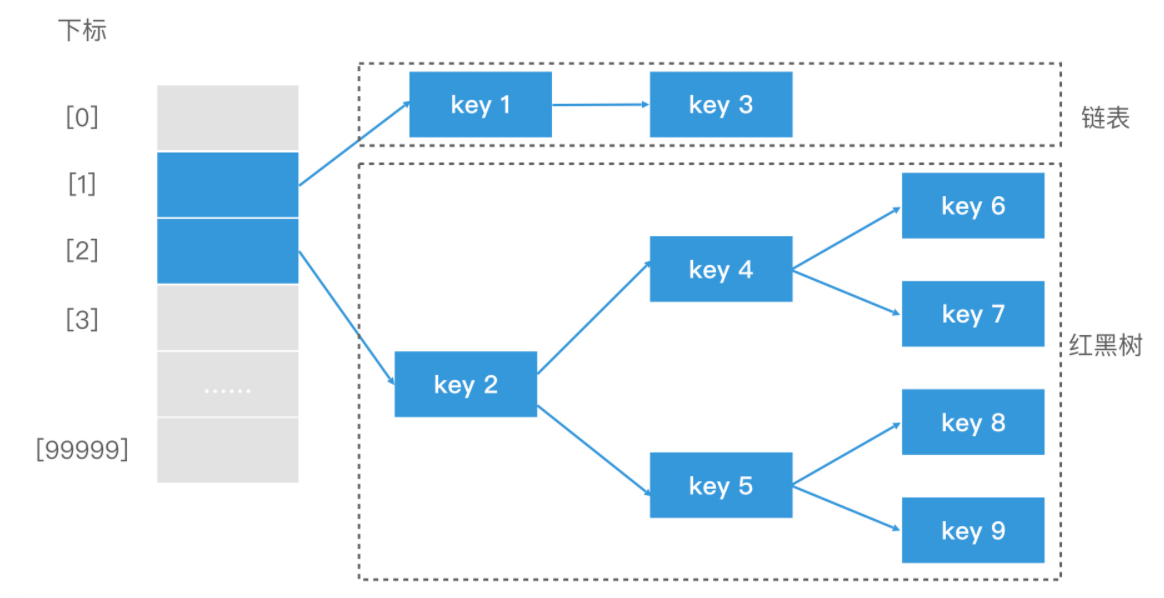
如果链表很长,遍历代价还是会很高。在 JDK1.8 之后,Java 中 HashMap 的实现就是在链表到了一定的长度时,将它转为红黑树;而当红黑树中的节点低于一定阈值时,就将它退化为链表。
哈希表的缺点
哈希表接近 O(1) 的检索效率是有前提条件的,就是哈希表要足够大和有足够的空闲位置,否则就会非常容易发生冲突。我们一般用装载因子(load factor)来表示哈希表的填充率。装载因子 = 哈希表中元素个数 / 哈希表的长度。
如果频繁发生冲突,大部分的数据会被持续地添加到链表或二叉检索树中,检索也会发生在链表或者二叉检索树中,这样检索效率就会退化。因此,为了保证哈希表的检索效率,我们需要预估哈希表中的数据量,提前生成足够大的哈希表。按经验来说,我们一般要预留一半以上的空闲位置,哈希表才会有足够优秀的检索效率。这就让哈希表和有序数组、二叉检索树相比,需要的存储空间更多了。
并且不利于遍历,因为失去”有序存储”的特点,如果需要遍历数据,或者进行范围查询,哈希表本身是没有什么加速办法的。For example,如果我们在一个很大的哈希表中存储了少数的几个元素,为了知道存储了哪些元素,我们只能从哈希表的第一个位置开始遍历,直到结尾,这样性能并不好。
Q&A
假设一个哈希表是使用开放寻址法实现的,如果我们需要删除其中一个元素,可以直接删除吗?为什么呢?如果这个哈希表是使用链表法实现的会有不同吗?
可以用open addressing方法。 在删除元素的时候 不会真正的删除,会有一个flag记录状态。后续插入新的元素还能用。否则就会导致每次就要重新申请内存,rehash,计算量太大。链表法的话,删除的是对应的node ,时间复杂度是O(1) 所以删除很快
通过开放寻址法是不可以简单的删除元素的,如果要删除的元素是通过寻址法找的存储下标,那么该元素所在的下标不是本身 hash 后的位置
链表法是可以的:因为元素本身的 hash 值和存储位置的下标 值是一致的